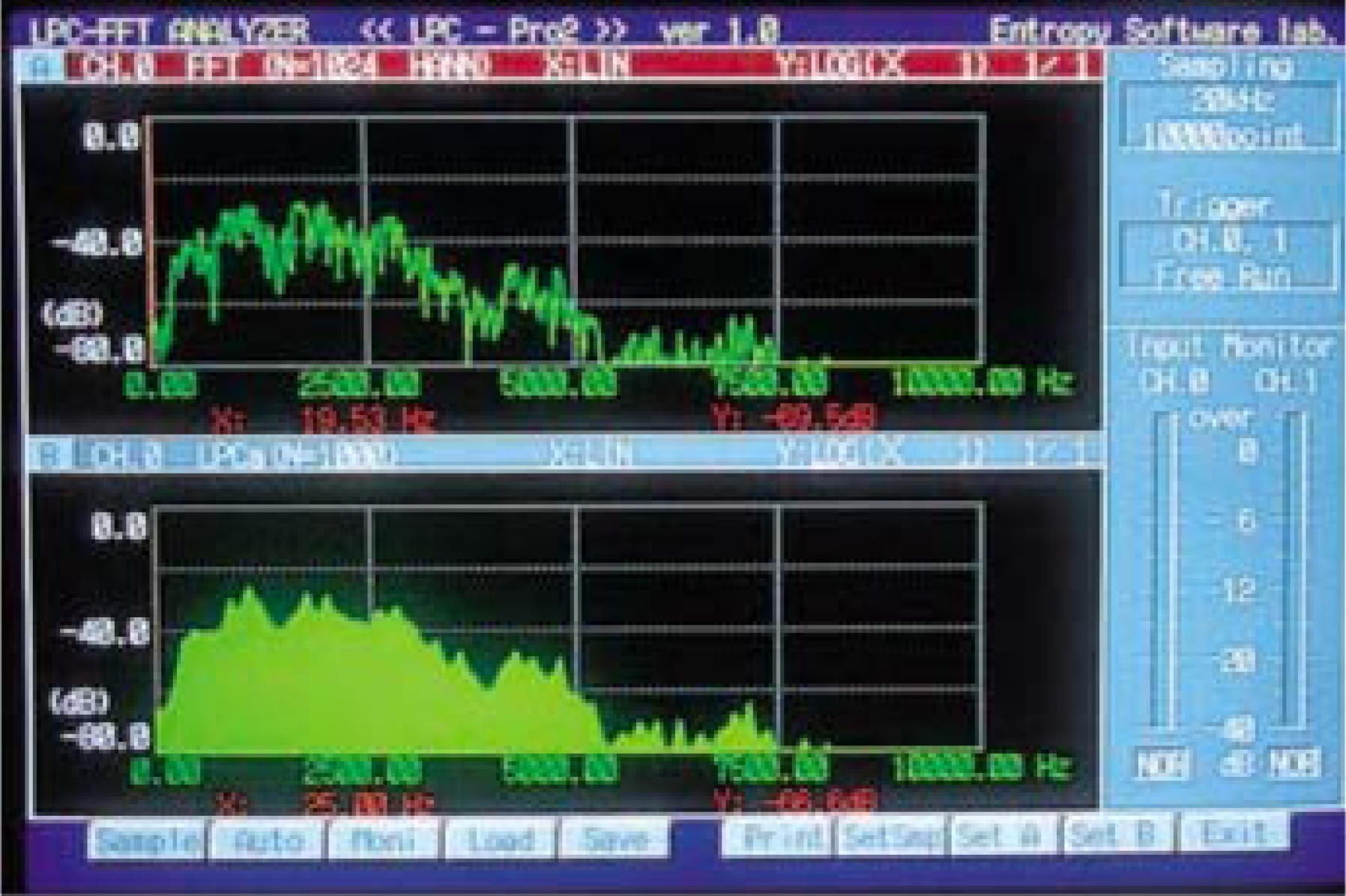
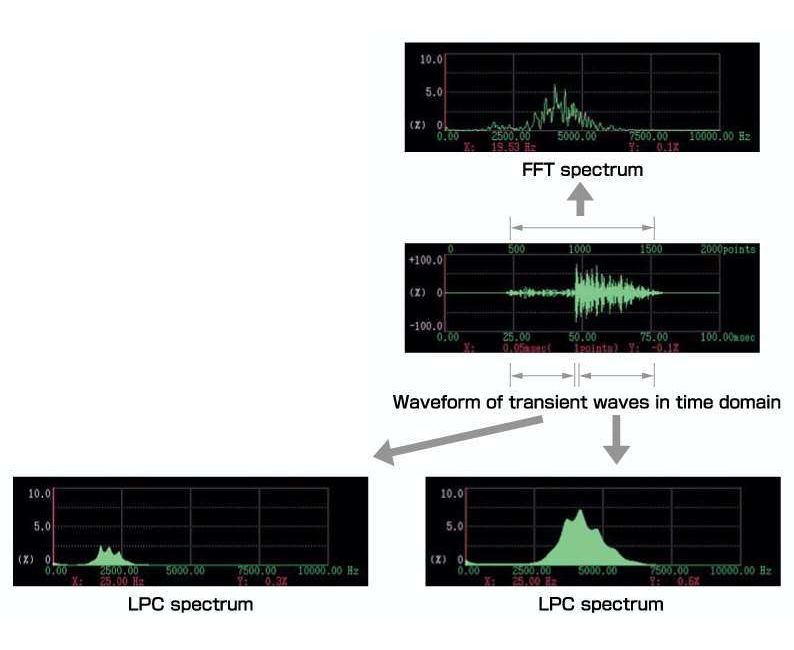
多くの場合、計算量の少ないFFTが音響スペクトルパターンの算出に用いられています。しかし、図1の上段に示すように、FFTスペクトルの形状には強い波うち(リップル)が発生するため、これを直接的に音響認識に用いた場合、認識率の低下が発生すると考えられています。さらに、FFTは長い定常信号には有効ですが、短い過渡信号に適用した場合にはスペクトル精度が低下することが知られています。
一方、LPC(Linear Predictive Coefficient 線形予測係数)は過渡信号に適した手法であり、図1の下段に示すようにLPCスペクトルの形状には波うち(リップル)は発生しません。LPCは計算量が多いという問題がありましたが、本製品は、マルチCPUを用いた64ビット並列処理を実行することにより、LPCスペクトルのリアルタイム処理を実現しました。
LPCスペクトル分析とは
1967年、Burgは地震波の解析のために、MEM(最大エントロピー法)と呼ばれる新しいスペクトル分析法を発表しました。このMEMは地震波のような過渡信号からも高分解能スペクトルが得られる特徴をもち、1970年ごろから地磁気変動や太陽周期、また音声認識の研究にも利用されるようになりました。
これらの研究の過程で、MEMはAR(自己回帰式)、LPC(線形予測係数)とも呼ばれるようになりましたが、計算量が多くリアルタイム処理ができなかったため一般の分野には普及しませんでした。
ここにきて、近年のマイクロプロセッサの高速化は著しく、LPCスペクトル分析のリアルタイム処理が可能となりました。今後は多くの分野においてLPCの応用が期待されています。
各スペクトル分析法の特徴
デジタル信号処理の分野では、1965年に発表されたFFT法と、1967年に発表されたLPC法の2つのスペクトル分析法が有名です。
FFTの特徴
高速フーリエ変換(Fast Fourier Transform)
計算量は少ないが、波形データの長さがT秒のときの周波数分解能は⊿f=(1/T)Hzになるため、FFTは波形データ長Tが長い定常信号の分析に適する。
LPCの特徴
線形予測係数(Linear Predictive Coefficient)
波形データの長さTに無関係に周波数分解能⊿fが決められるが、計算量が多いため、LPCは波形データ長Tが短い過渡信号の分析に適する。
LPCスペクトルアナライザソフトウェア
LPCスペクトルアナライザ・プログラムメニュー
LPC 1-d
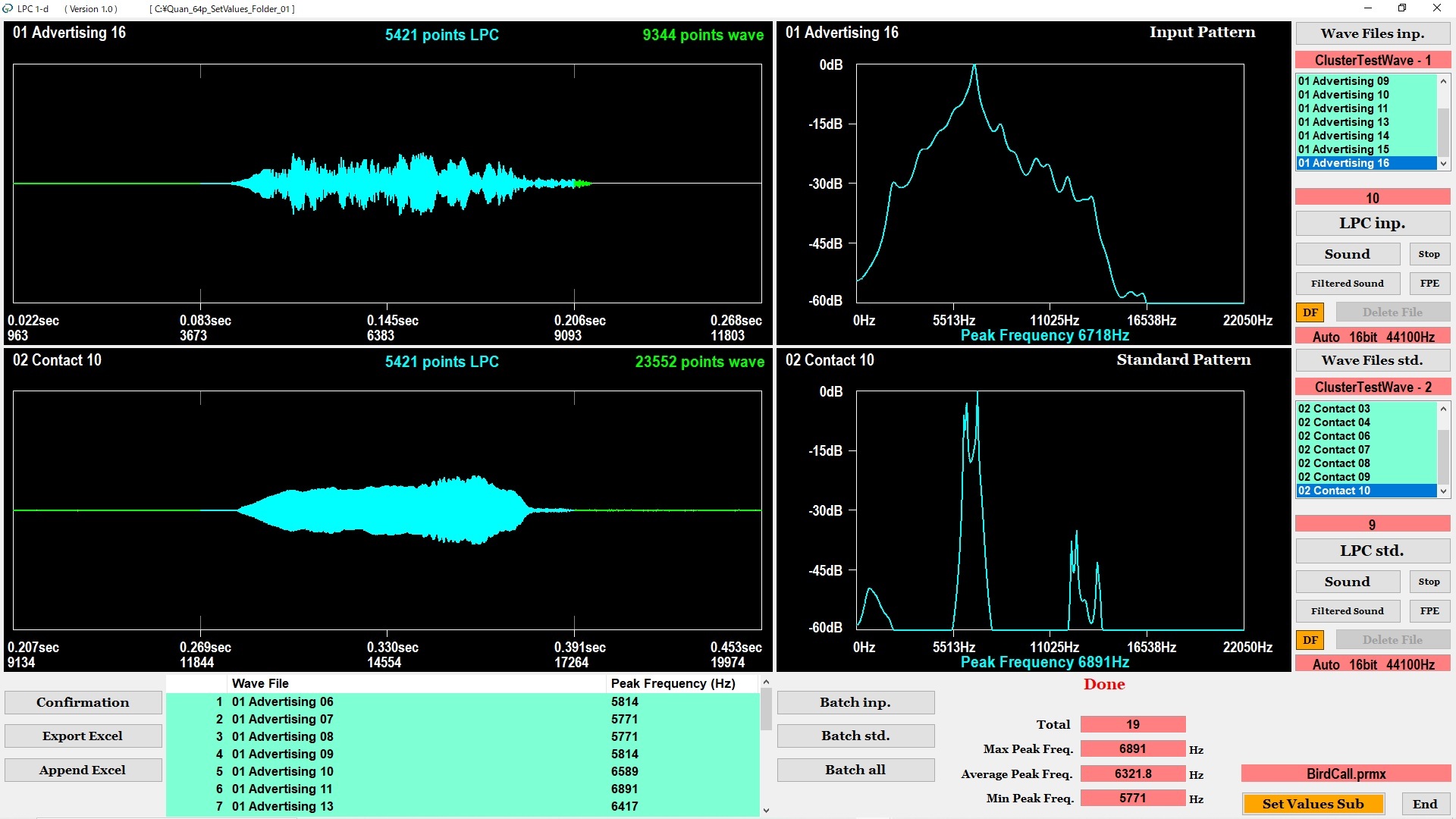
図6に示す画面の上段に、1番目のクラスタの中から選択したWAVファイルの音響波形と1次元LPCスペクトルが表示されます。同様に、画面の中段に、2番目のクラスタの中から選択したWAVファイルの音響波形と1次元LPCスペクトルが表示されます。なお、画面には、FIRデジタルフィルタ処理後の音響波形が表示されます。1次元LPCスペクトルは、それぞれの音響波形の水色(シアン)の部分から抽出されます。
画面の上段と中段に表示された2つの1次元LPCスペクトルを比較することが可能です。また、画面の下段に、すべてのWAVファイルについて、1次元LPCスペクトルのピーク周波数の一覧が表示されます。
LPC 2-d
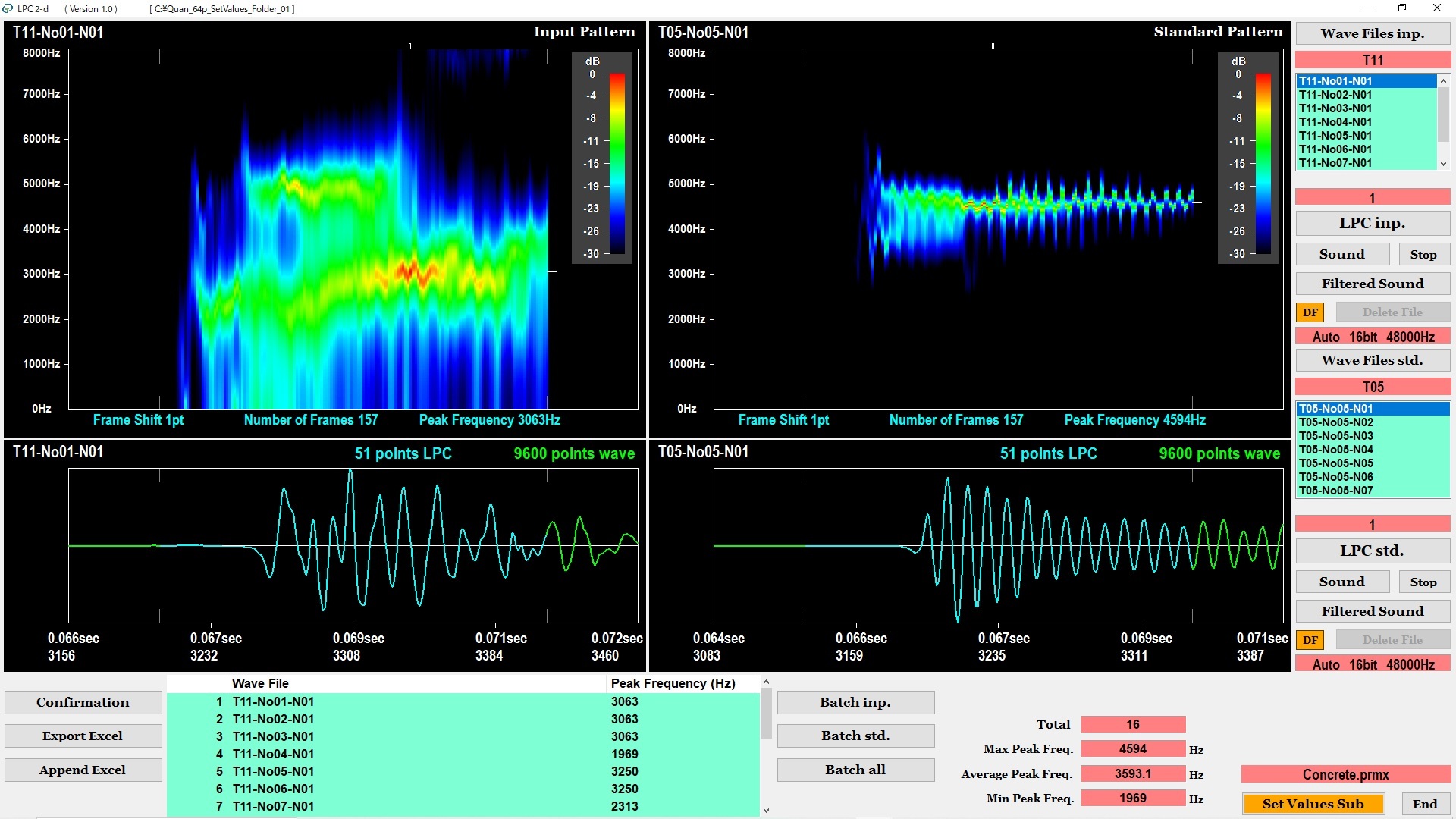
図7に示す画面の左側に、1番目のクラスタの中から選択したWAVファイルの音響波形と2次元LPCスペクトルが表示されます。同様に、画面の右側に、2番目のクラスタの中から選択したWAVファイルの音響波形と2次元LPCスペクトルが表示されます。なお、画面には、FIRデジタルフィルタ処理後の音響波形が表示されます。2次元LPCスペクトルは、それぞれの音響波形の水色(シアン)の部分から抽出されます。
画面の左側と右側に表示された2つの2次元LPCスペクトルを比較することが可能です。また、画面の下段に、すべてのWAVファイルについて、2次元LPCスペクトルのピーク周波数の一覧が表示されます。
Sonogram View
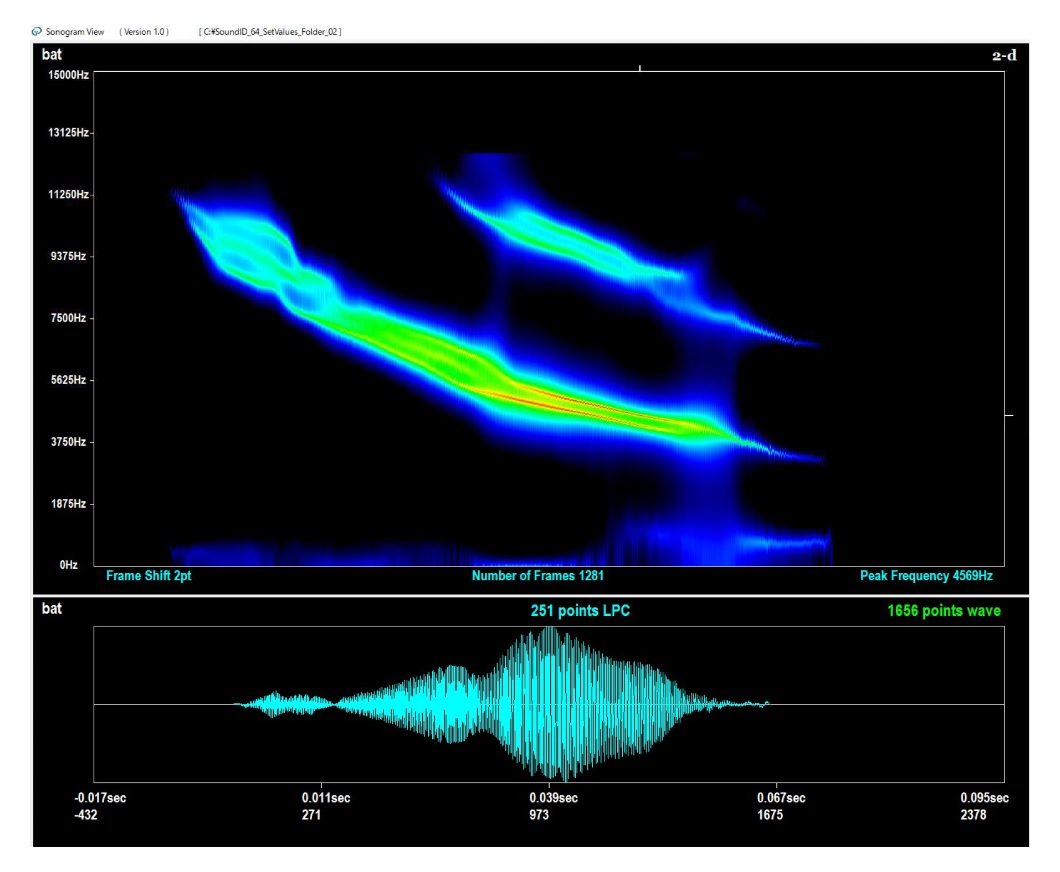
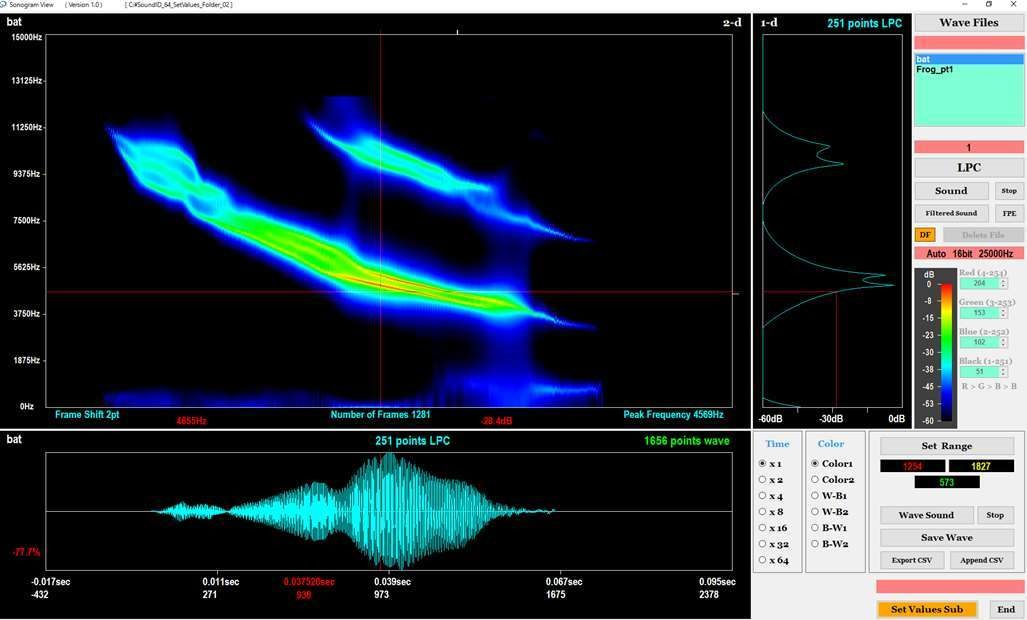
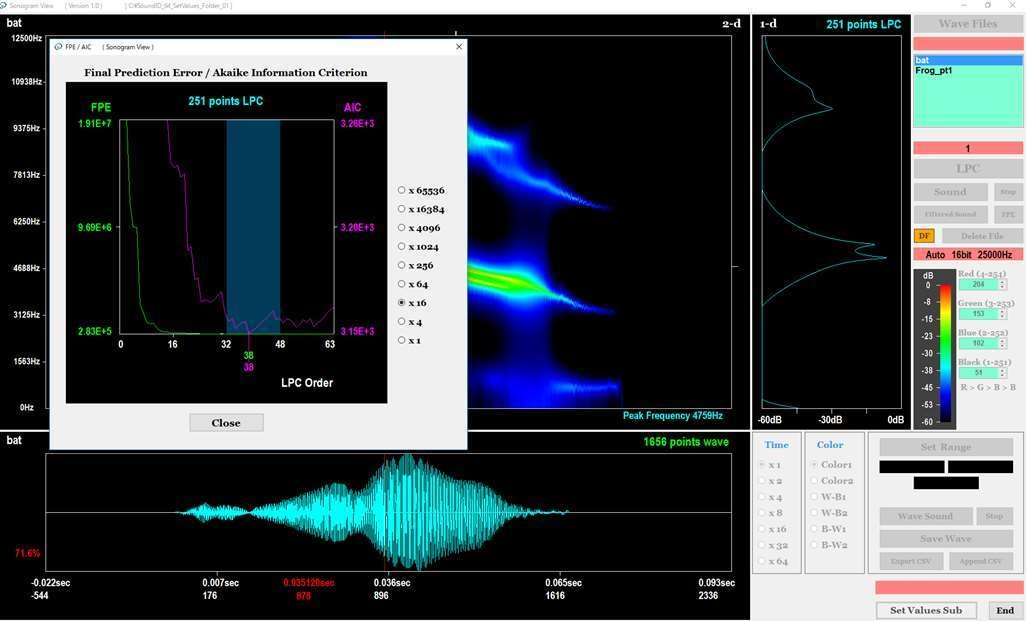
図8に示す画面の中央に、クラスタの中から選択したWAVファイルの音響波形とソノグラムが表示されます。なお、画面には、FIRデジタルフィルタ処理後の音響波形が表示されます。ソノグラムは、音響波形の水色(シアン)の部分から抽出されます。
ソノグラムの拡大表示、スクロール表示、モノクロ表示なども可能です。また、画面の中央においてマウスを用いて赤色の縦線を設定したとき、縦線の位置におけるソノグラムの断面が、1次元LPCスペクトルとして画面の右側に表示されます。さらに、この1次元LPCスペクトルのFPE(Final Prediction Error 最終予測誤差)及びAIC(Akaike Information Criterion 赤池情報量規準)が、図9に示すウィンドウに表示されます。
LPCスペクトルでは、ユーザーが任意に周波数分解能⊿fを決めることができます。本ソフトウェアでは、LPCスペクトルを697ピクセルにより画面表示していますので、次の計算式により周波数分解能⊿fが決まります。
(例1)
表示する上限周波数 LPC Freq.2 = 60000Hz
表示する下限周波数 LPC Freq.1 = 40000Hz のとき
周波数分解能⊿f = ( 60000Hz – 40000Hz )/( 697 – 1 ) = 28.74Hz
(例2)
表示する上限周波数 LPC Freq.2 = 52000Hz
表示する下限周波数 LPC Freq.1 = 48000Hz のとき
周波数分解能⊿f = ( 52000Hz – 48000Hz )/( 697 – 1 ) = 5.75Hz
Segmentation
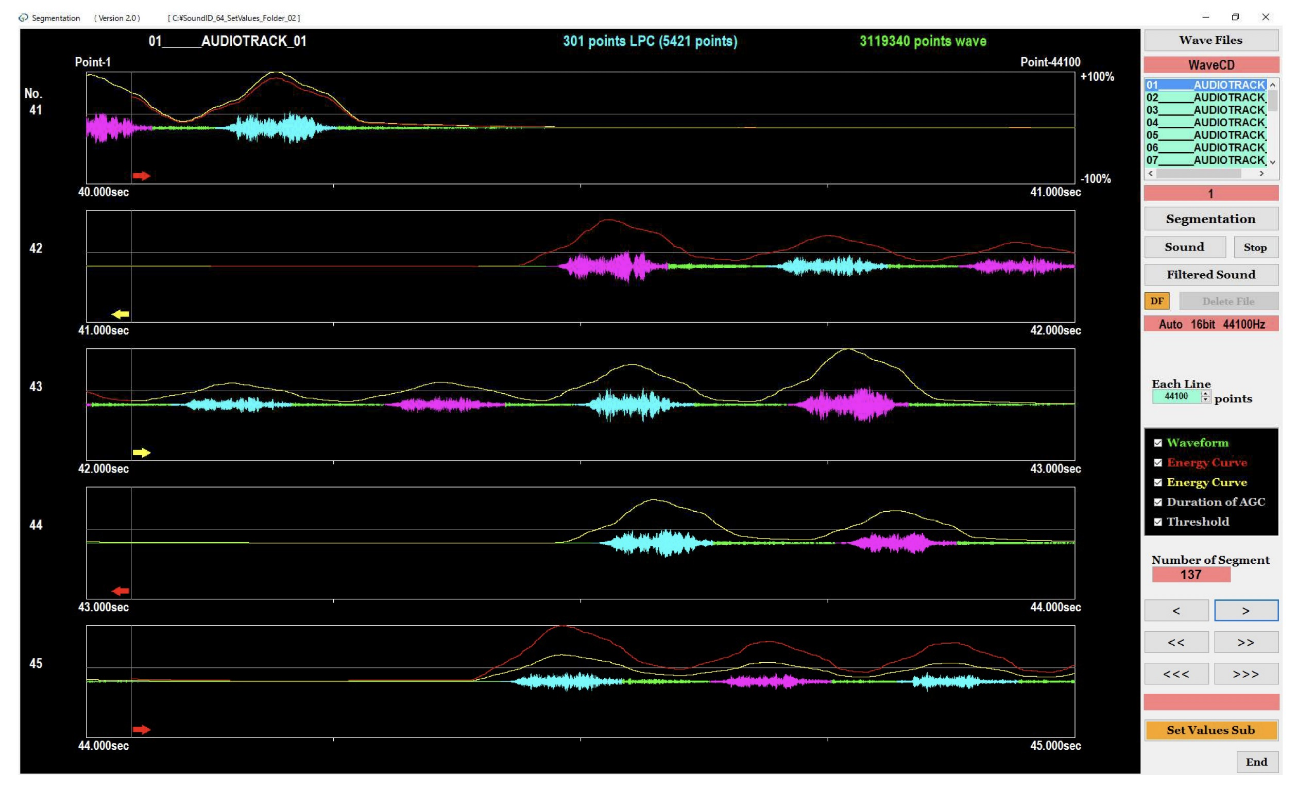
図10に示す画面に、連続録音データから自動的に目的の音響波形を切り出すセグメンテーションの処理結果が表示されます。1次元LPCスペクトル、2次元LPCスペクトル、ソノグラムの表示ソフトウェアにおける音響波形の切り出しを確認することができます。また、処理の高速化のために、認識ソフトウェアは図10の表示を省略しますので、セグメンテーションの処理結果はこの画面を用いて確認できます。
図11は、近接した目的音の切り出しの処理結果を示しています。近接した目的音を区別するために、2つの色(マゼンタとシアン)を交互に用いて目的音が表示されます。LPCスペクトルは、音響波形のマゼンタ色とシアン色のそれぞれの部分から抽出されます。
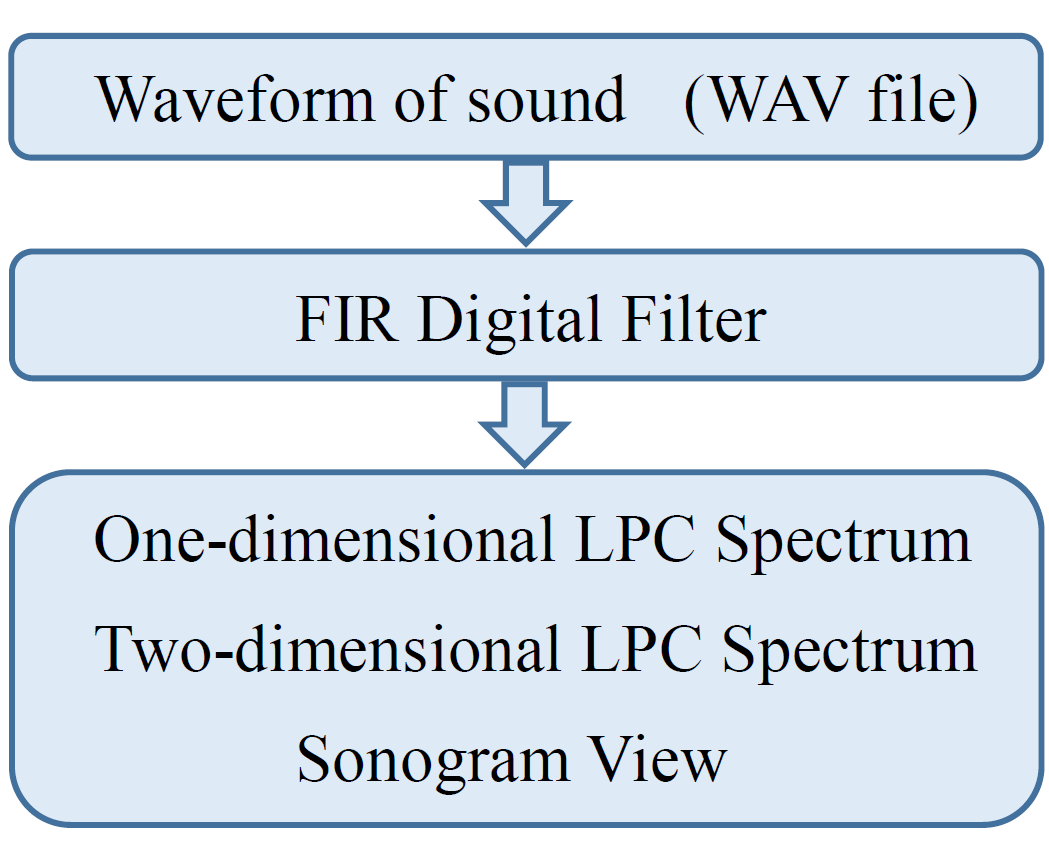
FIR Digital Filter
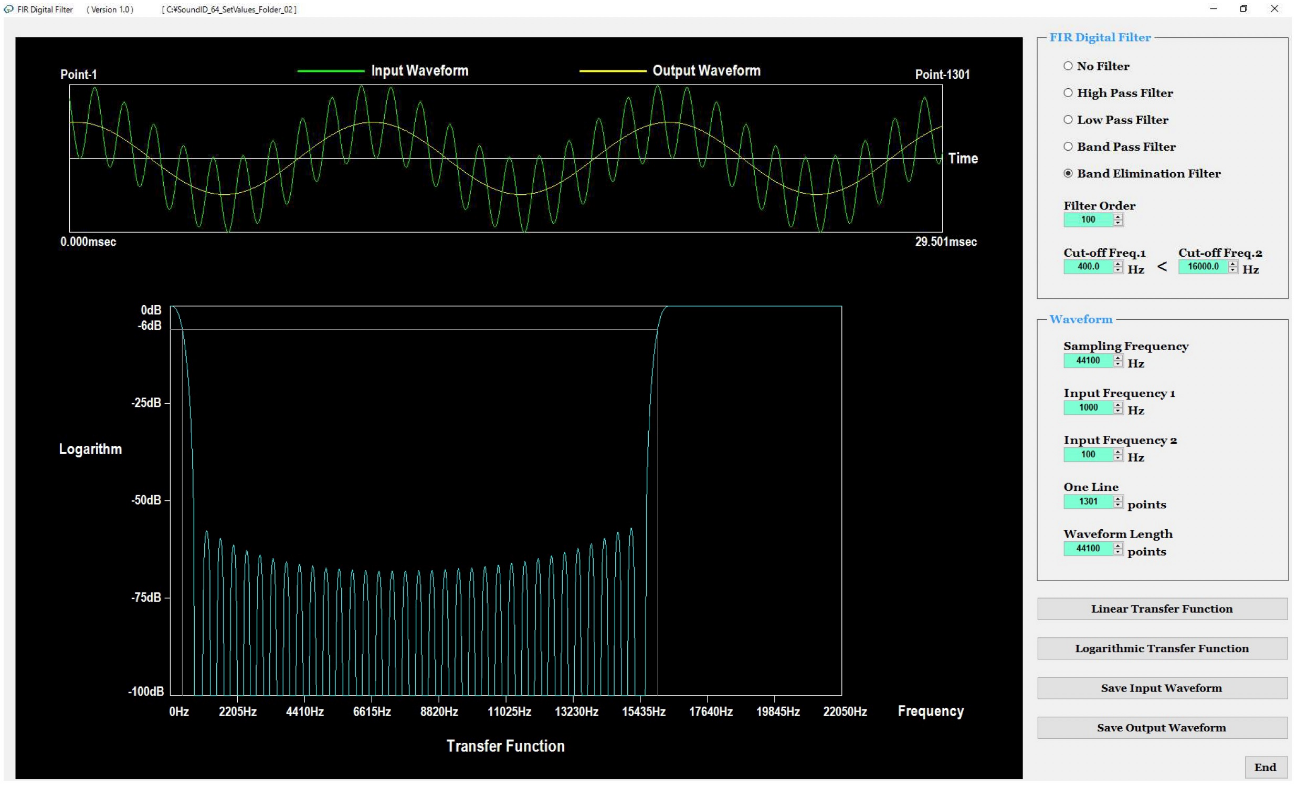
FIR(Finite Impulse Response)デジタルフィルタのシミュレーションソフトウェアです。図12に示す画面の右側上段において、フィルタの種類と特性値を設定します。また、画面の右側下段において、標本化周波数と2つの入力波の周波数を設定します。これら2つの入力波が加算されてFIRデジタルフィルタに入力されます。
図13は、FIRデジタルフィルタ、入力波(緑色)、出力波(黄色)の関係を模式的に示したものです。図12の画面の上段に、入力波形(緑色)と出力波形(黄色)が重ねて表示されます。また、図12の画面の下段に、FIRデジタルフィルタのLinear周波数特性/Log周波数特性が表示されます。
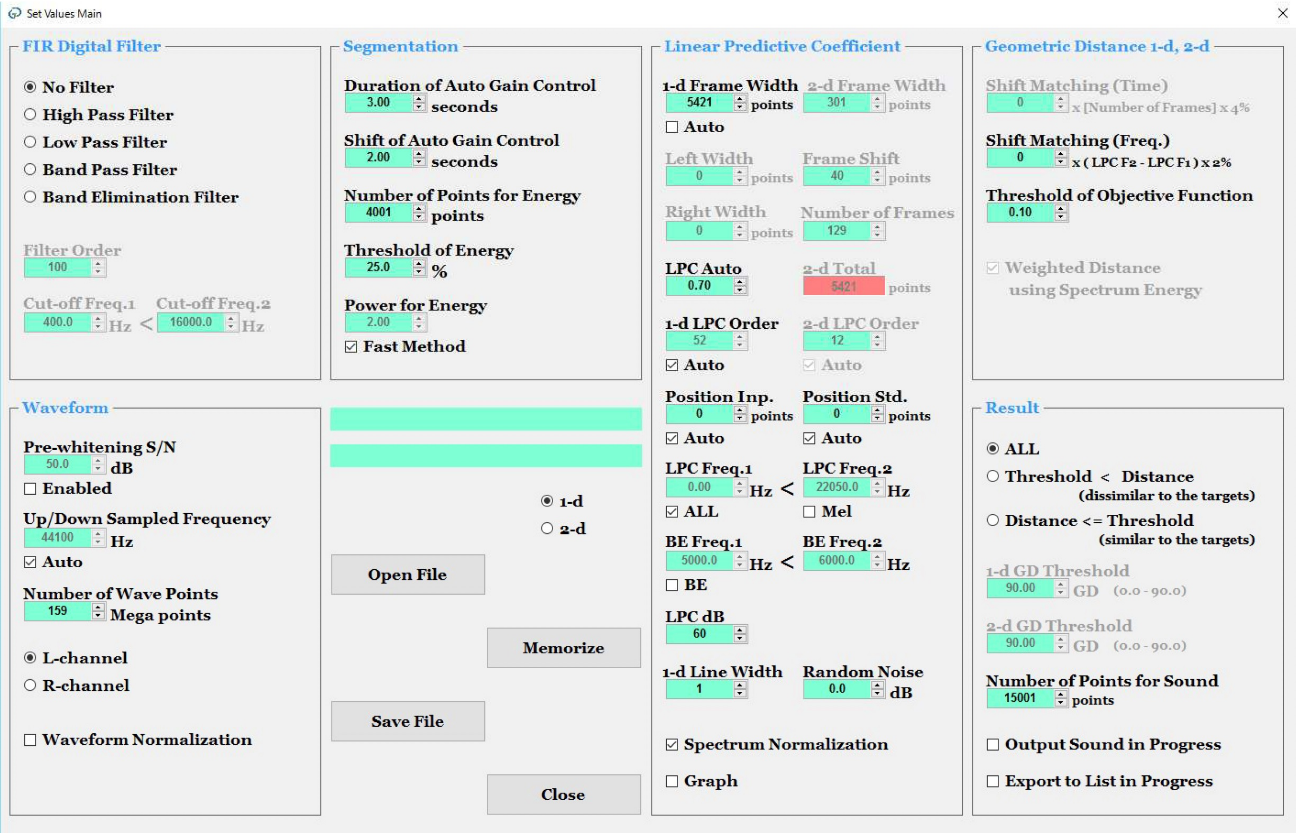
Set Values Main
基本性能
FIR Digital Filter
| Types of Filter | No Filter / High Pass Filter / Low Pass Filter / Band Pass Filter / Band Elimination Filter |
|---|---|
| Filter Order | 3 to 10000 |
| Cut-off Frequencies 1 and 2 | 0.0 Hz to ( sampling frequency / 2.0 ) Hz |
Waveform
| Pre-whitening S/N | Disenabled / Enabled 0.0 dB to 9999.0 dB |
|---|---|
| Up/Down Sampled Frequency | Auto / Manual 0 to 99999999 |
| Number of Wave Points | 10 Mega points to 1073 Mega points |
| Channel Selection | L-channel / R-channel |
| Waveform Normalization | Disenabled / Enabled |
Segmentation
| Duration of Auto Gain Control | 0.05 seconds to 99999999.00 seconds |
|---|---|
| Shift of Auto Gain Control | 0.01 seconds to 99999999.00 seconds |
| Number of Points for Energy | 1 point to 99999999 points |
| Threshold | 0.0 % to 100.0 % |
| Power for Energy | P = 0.10 to 6.00 , where |W(t)|^P P = 1 when you select “Fast Method” |
Linear Predictive Coefficient
| 1-d Frame Width / 2-d Frame Width | 5 points to 9999999 points |
|---|---|
| Frame Shift | 1 points to 99999999 points |
| Number of Frames | 7 to 99999 |
| 1-d LPC Order / 2-d LPC Order | 3 to 30000 |
| Position Input / Position Standard | -999999999 to 999999999 |
| LPC Frequencies 1 and 2 | 0.0 Hz to ( sampling frequency / 2.0 ) Hz |
| Band Elimination Frequencies 1 and 2 | 0.0 Hz to ( sampling frequency / 2.0 ) Hz |
| LPC dB | 1 dB to 1000 dB |
| 1-d Line Width | 1 to 9 |
| Random Noise | 0.0 dB to 99999999.0 dB |
| Spectrum Normalization | Disenabled / Enabled |
| Graph in Progress | Disenabled / Enabled |