畳み込みニューラルネットワーク(CNN)では、図1に示すように畳み込み層において入力画像とフィルタの間の類似度が計算されます。従来、類似の程度を測るためにコサイン尺度が広く使われています。
従来のコサイン尺度は2つのパターンをone-to-one mappingにより比較します。しかし、コサイン尺度はノイズに強く影響され、また、入力画像と標準画像(フィルタ)のピークにずれが発生したときには距離値が階段状に変化してしまいます。
この問題を改善するために、GDと呼ばれる新しい畳み込み法(類似性尺度)が開発されました。騒音環境下においてもGDは、従来のコサイン尺度よりも精度が高いことが確認されています。
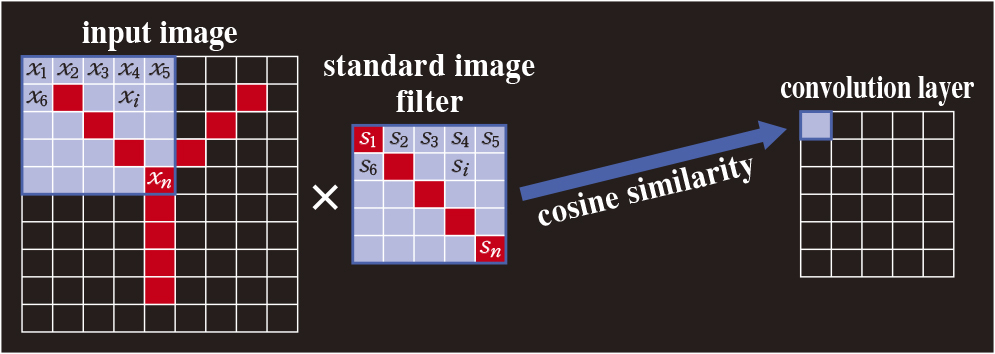
図1 入力画像とフィルタの畳み込み
従来の畳み込み法(コサイン尺度)
標準画像(標準音)の特徴量を成分si(i=1, 2,…, n)とする標準パターンベクトルsと、入力画像(入力音)の特徴量を成分xi(i=1, 2,…, n)とする入力パターンベクトルxを作成して、次式のように表現します。
このとき、従来のコサイン尺度は次式により算出されます。なお、図2B~5Bは、アークコサインを用いて算出される角度θを示しています。

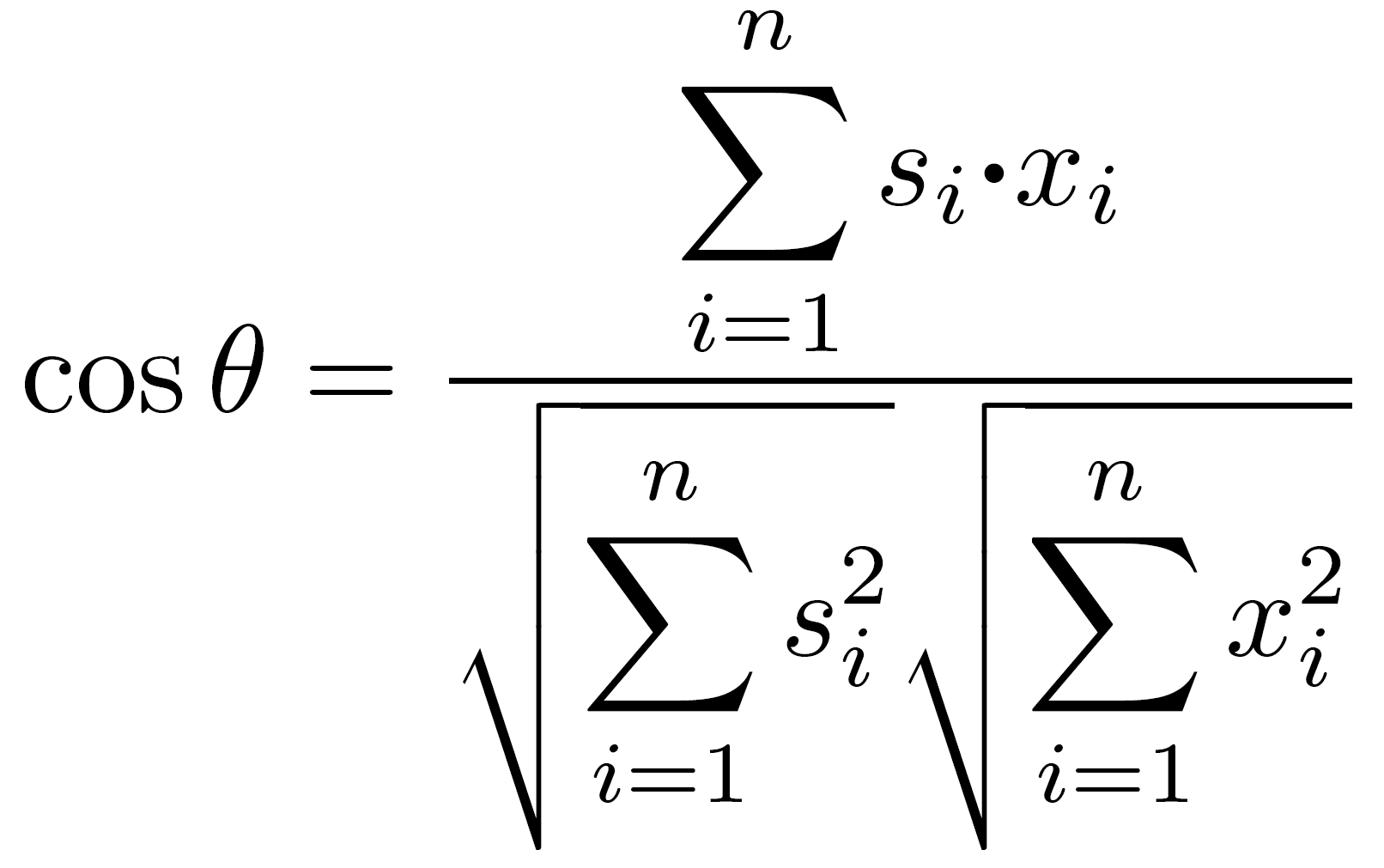
図2Aは、標準音としてパワースペクトルに2個のピークをもち、入力音1、2、3としてピーク位置がそれぞれ異なる例を示しています。なお、標準音のエネルギーと各入力音のエネルギーは等しくなっています。
図2Bの左の棒グラフは、標準音と各入力音1、2、3との間のコサイン尺度θ1、θ2、θ3を示していますが、従来のコサイン尺度ではθ1=θ2=θ3となるため、3つの入力音を区別できません。
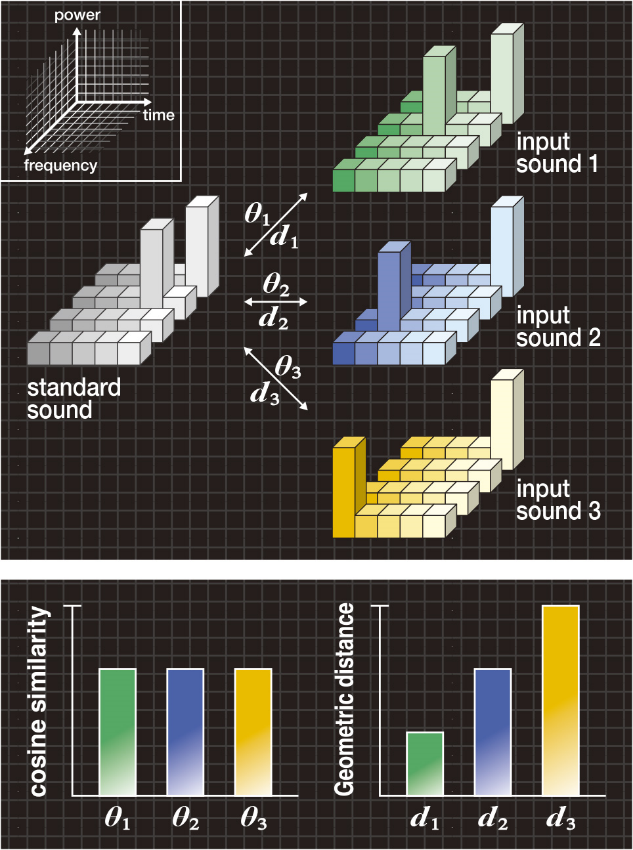
図2A(上段) 「ピークのずれ」の典型例
図2B(下段) コサイン尺度と形状距離
図3Aは、標準音として平坦なパワースペクトルをもち、入力音4、5として標準音に「スペクトル強度のゆらぎ」が発生し、入力音6として1個のピークをもつ例を示しています。ここで、各パワースペクトルには、変数αについて図中に示す関係があるため、標準音のエネルギーと各入力音のエネルギーは等しくなります。
図3Bの左の棒グラフは、標準音と各入力音4、5、6との間のコサイン尺度θ4、θ5、θ6を示していますが、従来のコサイン尺度ではθ4=θ5=θ6となるため、3つの入力音を区別できません。
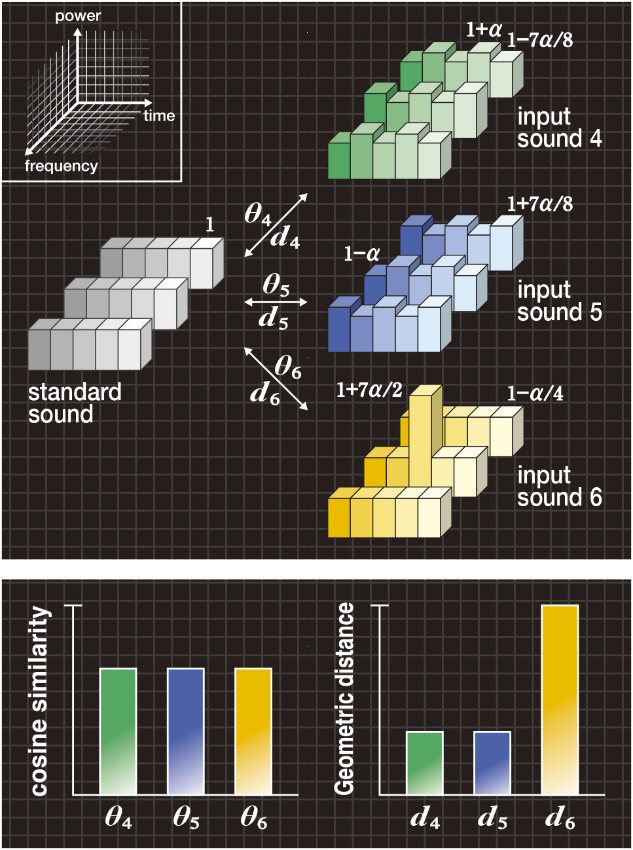
図3A(上段) 「ゆらぎ」の典型例
図3B(下段) コサイン尺度と形状距離
図4Aは、記号“+”の標準画像と、横線の位置がそれぞれ異なる入力画像1、2、3を示しています。
図4Bの左の棒グラフは、標準画像と各入力画像1、2、3との間のコサイン尺度θ1、θ2、θ3を示していますが、従来のコサイン尺度ではθ1=θ2=θ3となるため、3つの入力画像を区別できません。
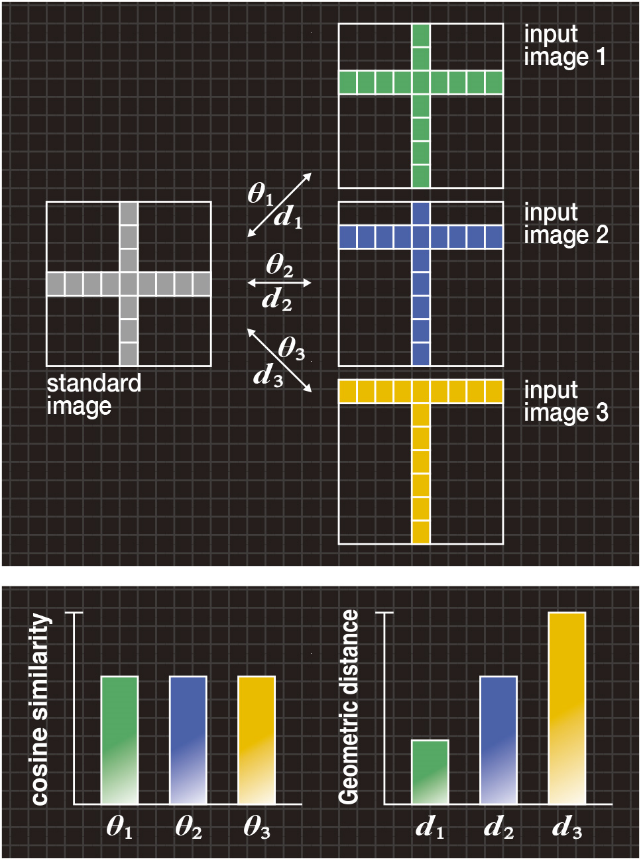
図4A(上段) 「位置ずれ」の典型例
図4B(下段) コサイン尺度と形状距離
図5Aは、アルファベット“E”の標準画像と、それぞれ“E”、“F”、“G”の入力画像4、5、6を示しています。
図5Bの左の棒グラフは、標準画像と各入力画像4、5、6との間のコサイン尺度θ4、θ5、θ6を示していますが、従来のコサイン尺度ではθ4>θ5>θ6となるため、アルファベット“E”を正しく認識できません。
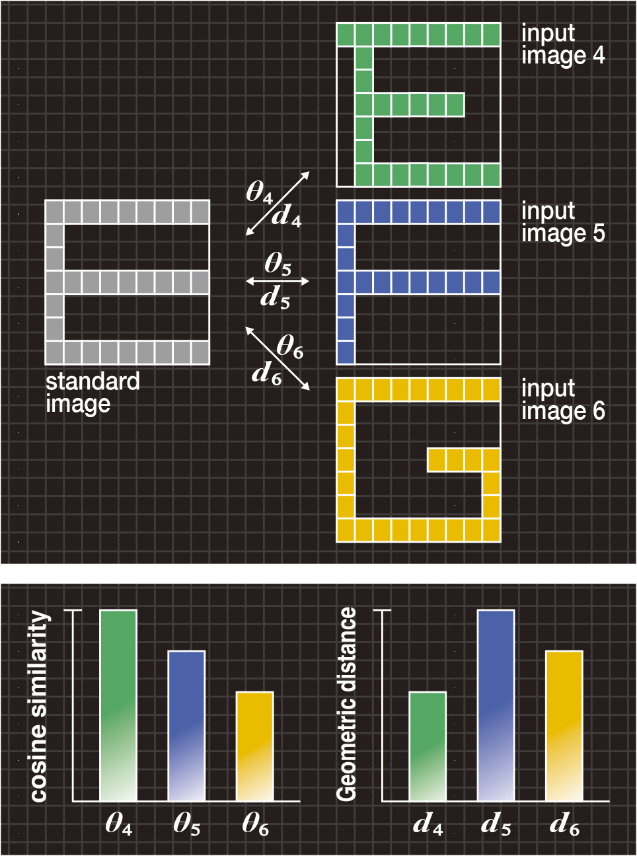
図5A(上段) 「文字の変形」の典型例
図5B(下段) コサイン尺度と形状距離
新しい畳み込み手法「GD」
新しい類似性尺度GDは、雑音などの「ゆらぎ」の中で標準パターンと入力パターンにピークの「ずれ」が生じたとき、「ゆらぎ」を吸収しながら「ずれ」の増加とともに単調増加します。
鳥の鳴き声
GDアルゴリズムの有効性を検証するため、” Macleay’s Fig-Parrot”と呼ばれる鳥の鳴き声の認識実験を行いました。次のビデオは、雑音環境下であっても、GDアルゴリズムを用いたパターンマッチングが正しい結果を出力することを示しています。
コンクリートの打音
腐食によるコンクリート内部の空洞位置を見つけるために、正常なコンクリートの表面を打撃して得られる標準音、および、内部に空洞のあるコンクリートの表面を打撃して得られる標準音を登録しておき、それらを入力音と比較します。
次のビデオは、GDアルゴリズムを用いて、空洞のあるコンクリート20個のうち17個の異常を検出できることを示しています。


